トレーニングおよび検出データの要件

データ形式と品質要件

トレーニングおよびテスト・データは、特定のタイムスタンプで記録された複数の属性(シグナルやセンサーなど)からの値を次の日付順に表すために必要です。

• 最初の列としてタイムスタンプ、およびその後に他の数値属性、シグナルおよびセンサーを含む列。
• 各行は、特定のタイムスタンプでの属性、シグナルおよびセンサーの1つの観察を表します。

これらの要件により、トレーニングが成功し、トレーニングされたモデルが高品質であることが保証されます。

タイムスタンプ

• タイムスタンプ列はオプションです。各値行にタイムスタンプが指定されているか、まったく指定されていません。
  • タイムスタンプ列を指定する場合は、最初の列にtimestamp (空白なしのすべて小文字)という名前を付ける必要があります。
  • データ内のタイムスタンプは順番に増加しており、重複がない可能性があります。
  • タイムスタンプには、異なる頻度を指定できます。たとえば、1時間で50回の観測を行い、次の1時間で200回の観測を行えます。
• タイムスタンプが指定されていない場合、データは時間によって時系列順にソートされるとみなされます。

属性

• 値が欠落している場合があり、そのときはnullとして表す必要があります。

• 属性、シグナルおよびセンサーの列全体で、すべての値を欠落値として指定することはできません。

• 属性名は一意である必要があります。属性の合計数は300より大きくすることはできません。

• シグナル名とセンサー名は、MSETにすることはできません。

• センサーと信号が相関していない場合、サービスはすべての単変量モデルを構築します。

• ウィンドウ・サイズは、単変量モデルに対してのみ有効な概念です。

トレーニング

• トレーニング・データの観測およびタイムスタンプの数は、少なくとも8 × 属性数、または80のいずれか大きい方である必要があります。

• シグナル名とセンサー名は、MSETにすることはできません。

• センサーとシグナルが相関していない場合、サービスはすべての単変量モデルを構築します。

• ウィンドウ・サイズは、単変量モデルに対してのみ有効な概念です。

たとえば、100個のセンサーの場合、必要な最小行数はMax(8 x 100, 80) = 800行です。センサーが4個の場合、必要な最小行はMax(8 × 4, 80) = 80行です。

ノート

デフォルトでは、モデル・トレーニングは単変量アルゴリズムを使用して行われます。

検出

ユースケースに応じて、同期検出または非同期検出を使用できます。

• 単変量モデルの場合、行のウィンドウ・サイズ- 1は異常では検出されません。

• windowSize行より少ない行を指定した場合、単変量シグナルに対して異常検出は発生しません。

• データ・ポイントは、シグナル数を行数で乗算した値です。

同期検出

• 検出データセットが30,000データ・ポイントより小さく、時間依存の場合に使用します。
• バッチ検出コールでは、検出ペイロードの最大サイズは、シグナルの場合は最大300、シグナルと行の任意の組合せの場合は最大30,000データ・ポイントです。

ジョブを使用した非同期検出

• 検出データセットが30,000データポイントよりも大きく、時間の制約がない場合に使用します。
• 非同期検出ジョブの場合、検出ペイロードの最大サイズはリクエストのタイプによって異なります。
  • インライン・リクエスト入力の場合、リクエストの最大サイズは11MBおよび500,000データ・ポイントに制限されます。
  • Object Storageの入力の場合、ファイルの最大サイズは500MBおよび1000万データ・ポイントに制限されています。

データ準備

MSETでは、データの準備は、モデルのトレーニングに使用されるデータがクリーンで一貫性があり、分析に適切であることを確認するために不可欠です。次に、異常検出で使用するためのPythonを使用した、いくつかの共通技術の概要と対応する例を示します。

四分位範囲(IQR)

IQRは、時系列データの外れ値の識別と削除に使用する統計分散の尺度です。IQRは、75パーセンタイル(Q3)と25パーセンタイル(Q1)のデータの差異として計算されます。外れ値は、データ値と上限と下限を比較して識別できます。上限は、それぞれQ3 + 1.5 * IQRおよびQ1 - 1.5 * IQRとして計算されます。次に例を示します:

• 入力: time_series_data - 時系列データを含むNumPy配列またはパンダ・シリーズ。
• 出力: cleaned_data - 外れ値が削除されたクリーンな時系列データを含むNumPy配列またはパンダ・シリーズ。

Pythonの例:

import numpy as np

# Generate some example time series data
time_series_data = np.random.normal(0, 1, 100)

# Calculate the IQR
Q1 = np.percentile(time_series_data, 25)
Q3 = np.percentile(time_series_data, 75)
IQR = Q3 - Q1

# Define the upper and lower bounds for outlier detection
upper_bound = Q3 + 1.5 * IQR
lower_bound = Q1 - 1.5 * IQR

# Identify and remove outliers
outliers = (time_series_data < lower_bound) | (time_series_data > upper_bound)
cleaned_data = time_series_data[~outliers]

外れ値検出

Zスコア、移動平均、機械学習ベースの手法など、時系列データの外れ値検出には様々な方法を使用できます。分離フォレスト・アルゴリズムは、監視なし異常検出に適した機械学習ベースのアプローチです。次に例を示します:

• 入力: time_series_data - 時系列データを含むNumPy配列またはパンダ・シリーズ。
• 出力: cleaned_data - 外れ値が削除されたクリーンな時系列データを含むNumPy配列またはパンダ・シリーズ。

Pythonの例:

import numpy as np
from sklearn.ensemble import IsolationForest

# Generate some example time series data
time_series_data = np.random.normal(0, 1, 100)

# Train the Isolation Forest model
model = IsolationForest(contamination=0.05)  # Specify the contamination level (i.e., expected proportion of outliers)
model.fit(time_series_data.reshape(-1, 1))

# Predict outlier labels
outlier_labels = model.predict(time_series_data.reshape(-1, 1))

# Extract the clean data
cleaned_data = time_series_data[outlier_labels == 1]

高相関シグナルの処理

相関性の高いシグナルによる時系列分析のデータ準備には、変数間の相関を処理するためのいくつかの重要なステップが含まれます。一般的な手法は次のとおりです。

1. データの正規化:時系列データを正規化して、すべての変数のスケールが同じになるようにすることが重要です。これは、高い相関関係を持つ変数を効果的に比較および分析するのに役立ちます。最小最大スケーリングやZスコアの正規化などの正規化方法を使用して、変数を同様の範囲にすることができます。

2. 機能選択:ピアソン相関係数を使用して、相関が高い変数を識別し、冗長な機能を削除します。たとえば、相関係数のしきい値を設定し、相関性の高い変数のペアから1つの変数のみを保持できます。

   1. ピアソン相関係数の計算:変数間の線形相関の強度と方向を測定するための一般的な手法の1つは、ピアソン相関係数です。ピアソン相関係数は、2つの変数間の線形関係を測定し、-1 (完全否定相関)から1 (完全正相関)までの範囲の値と0 (相関なし)の範囲の値を示します。Pythonのscipy.statsモジュールの pearsonr functionを使用して、ピアソン相関係数を計算できます。次に、Pythonでのデータ準備のためのピアソン相関係数の使用例を示します:

      import numpy as np 
      from scipy.stats import pearsonr  
      
      # Generate some example time series data with two highly correlated signals A and B 
      np.random.seed(0) A = np.random.normal(0, 1, 100) 
      B = A + np.random.normal(0, 0.1, 100)  
      
      # Calculate Pearson correlation coefficient between A and B 
      correlation_coefficient, _ = pearsonr(A, B) 
      print(f"Pearson correlation coefficient between A and B: {correlation_coefficient:.2f}")

   

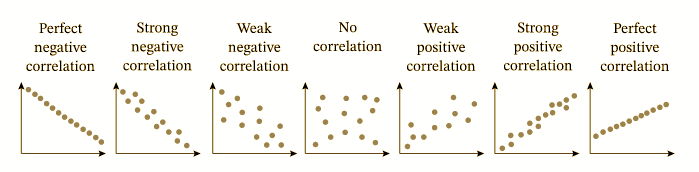
3. ディメンションの削減:プリンシパル・コンポーネント分析や特異値分解などの手法を使用して、時系列データのディメンション性を削減し、相関しない変数のセットを作成できます。これは、元の変数からのほとんどの情報を保持しながら、主コンポーネントとも呼ばれます。

その他の推奨事項

• 将来、新しい属性が追加された場合は、検出時にそれを考慮するために、新しい属性ラベルを含むデータを再度トレーニングする必要があります。

• 属性がトレーニング中に別のシグナルの複製として検出された場合、その属性は自動的に削除されます。

• 検出コールのデータの増加は、最大許容データの制限内にあるかぎり有効です。

データ形式の要件

異常検出サービスでは、タイムスタンプおよび数値属性を持つデータを含むCSVおよびJSONファイル形式がサポートされています。

また、ATPおよびInfluxDBからのデータもサポートしています。このデータは、タイムスタンプの数と形式、数値属性の数に関して要件が似ています。

CSV形式

各列はセンサー・データを表し、行は特定のタイムスタンプの各センサーに対応する値を表します。

CSV形式のデータには、カンマ区切りの行が必要です。最初の行はヘッダー、他の行はデータです。異常検出サービスでは、タイムスタンプを指定するときに、最初の列の名前がtimestampである必要があります。

次に例を示します:

timestamp,sensor1,sensor2,sensor3,sensor4,sensor5
2020-07-13T14:03:46Z,,0.6459,-0.0016,-0.6792,0
2020-07-13T14:04:46Z,0.1756,-0.5364,-0.1524,-0.6792,1
2020-07-13T14:05:46Z,0.4132,-0.029,,0.679,0

ノート

• 欠落値は許可され(null)、データはタイムスタンプでソートされ、ブール・フラグ値は数値(0または1)に変換する必要があります。

• 最後の行を改行することはできません。最後の行は、他のシグナルでの観測です。

JSON形式

同様に、JSON形式のデータにも、タイムスタンプと数値属性のみが含まれている必要があります。次のキーを使用します:

{ "requestType": "INLINE",
  "signalNames": ["sensor1", "sensor2", "sensor3", "sensor4", "sensor5", "sensor6", "sensor7", "sensor8", "sensor9", "sensor10"],
  "data": [
      { "timestamp" : "2012-01-01T08:01:01.000Z", "values" : [1, 2.2, 3, 1, 2.2, 3, 1, 2.2, null, 4] },
      { "timestamp" : "2012-01-02T08:01:02.000Z", "values" : [1, 2.2, 3, 1, 2.2, 3, 1, 2.2, 3, null] }
  ]
}

ノート

欠落値は引用符なしでnullとしてコード化されています。